曲率公式,曲线弯曲程度的数学表达

曲率（Curvature）是一个几何概念，用于描述曲线在某一点的弯曲程度。在二维空间中，曲率通常用κ表示。曲率的计算公式依赖于曲线的表示方式。以下是几种常见的曲率计算方法：

1. 直角坐标系中的曲率公式： 如果曲线由参数方程 qwe2, qwe2 表示，其中 是参数，那么在点 , yqwe2 qwe2 处的曲率公式为： g' f'g''|}{^2 g'^2qwe2^{3/2}} qwe2 如果曲线由显式方程 qwe2 表示，那么在点 qwe2 处的曲率公式为： |}{qwe2^2qwe2^{3/2}} qwe2

2. 极坐标系中的曲率公式： 如果曲线由极坐标方程 qwe2 表示，其中 是极角，那么在点 qwe2 处的曲率公式为： ^2} qwe2

3. 弧长参数化的曲率公式： 如果曲线由弧长参数 表示，那么在点 处的曲率公式为： |}{|T|} qwe2 其中 qwe2 是单位切向量， qwe2 是单位切向量的导数。

4. 空间曲线的曲率： 对于空间中的曲线，曲率通常分为两个部分：法曲率（Normal Curvature）和测地曲率（Geodesic Curvature）。法曲率描述曲线在垂直于曲线所在平面的方向上的弯曲程度，而测地曲率描述曲线在曲线所在平面内的弯曲程度。

这些公式是曲率的基本计算方法，但实际应用中可能需要根据具体情况选择合适的公式。

深入解析曲率公式：曲线弯曲程度的数学表达

曲率公式是高等数学中一个重要的概念，它描述了曲线在某一特定点的弯曲程度。本文将深入解析曲率公式的定义、推导过程以及在实际应用中的重要性。

曲率的定义

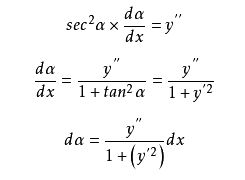
曲率是描述曲线弯曲程度的一个物理量，它反映了曲线偏离直线的程度。在数学上，曲率可以理解为曲线在某一点处的切线方向角对弧长的转动率。曲率越大，表示曲线在该点的弯曲程度越大。

曲率公式的推导

曲率公式的推导过程涉及到了微分学的知识。以下是一个简化的推导过程：

首先，我们假设曲线C可以用参数方程表示，即C(u) = (x(u), y(u), z(u))。

然后，我们求出曲线C在参数u处的切向量T(u)和法向量N(u)。

接着，我们求出曲线C在参数u处的曲率k(u)。

具体推导过程如下：

求切向量T(u)：T(u) = (x'(u), y'(u), z'(u))。

求法向量N(u)：N(u) = (y''(u), z''(u), -x''(u))，其中x''(u)、y''(u)、z''(u)分别为x(u)、y(u)、z(u)的二阶导数。

求曲率k(u)：k(u) = ||N(u)|| / ||T'(u)||，其中||N(u)||表示法向量N(u)的模长，||T'(u)||表示切向量T(u)的模长。

最终，我们得到曲率公式：k(u) = (x''(u)y''(u) - y'(u)z''(u)) / (||T(u)||^3)。

曲率公式的应用

曲率公式在实际应用中具有重要意义，以下列举几个例子：

在工程领域，曲率公式可以用来分析桥梁、道路等结构的弯曲程度，从而确保其安全性和稳定性。

在计算机图形学中，曲率公式可以用来优化曲线的形状，提高图形的渲染质量。

在物理学中，曲率公式可以用来研究物体在曲线运动过程中的受力情况。

总之，曲率公式在各个领域都有广泛的应用，它为人们研究曲线的弯曲程度提供了有力的数学工具。

曲率公式的拓展

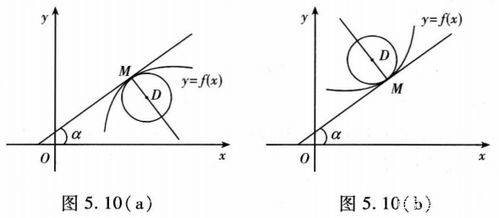
对于空间曲线，曲率公式可以表示为：k(u) = (x''(u)y''(u)z'''(u) - x'''(u)y''(u)z''(u) - x'(u)y'''(u)z''(u) x''(u)y'(u)z'''(u)) / (||T(u)||^3)。

对于参数方程表示的曲线，曲率公式可以表示为：k(u) = ||T'(u) × T''(u)|| / ||T(u)||^3，其中×表示向量积。

这些拓展内容使得曲率公式在空间曲线的研究中更加具有实用性。

曲率公式是描述曲线弯曲程度的重要数学工具，它为人们研究曲线的几何性质提供了有力的支持。通过对曲率公式的深入解析，我们可以更好地理解曲线的弯曲程度，并在实际应用中发挥其重要作用。