pid控制算法,原理、实现与应用
PID控制算法(ProportionalIntegralDerivative control)是一种常用的控制算法,广泛应用于工业控制系统中。它通过调节比例(P)、积分(I)和微分(D)三个参数来控制系统的输出,以达到期望的响应。
PID控制算法的基本原理是:
1. 比例(P)控制:根据当前误差的大小来调整控制量,误差越大,控制量越大。比例控制可以快速响应误差,但容易产生超调和振荡。
2. 积分(I)控制:根据误差的累积来调整控制量,误差累积越大,控制量越大。积分控制可以消除稳态误差,但响应速度较慢。
3. 微分(D)控制:根据误差的变化率来调整控制量,误差变化越快,控制量越大。微分控制可以预测误差的变化趋势,提高系统的稳定性。
PID控制算法的公式为:
$$u = K_p cdot e K_i cdot int_{0}^{t} e dtau K_d cdot frac{de}{dt}$$
其中:
$ u $ 是控制量 $ e $ 是误差,即期望值与实际值之差 $ K_p $ 是比例增益 $ K_i $ 是积分增益 $ K_d $ 是微分增益
在实际应用中,PID控制算法的参数需要根据具体系统进行调整,以达到最佳的控制效果。PID控制算法的优点是简单易用,适应性强,缺点是对于复杂的系统可能需要较长的调试时间。
除了基本的PID控制算法,还有一些改进的PID控制算法,如:
比例积分微分前馈(PIDF)控制:在PID控制的基础上增加前馈控制,提高系统的响应速度和稳定性。 自适应PID控制:根据系统的动态特性自动调整PID参数,提高系统的自适应能力。 模糊PID控制:将模糊控制与PID控制相结合,提高系统的鲁棒性和适应性。
PID控制算法是控制理论中最基本的控制算法之一,在工业控制、自动化控制等领域有着广泛的应用。
PID控制算法:原理、实现与应用
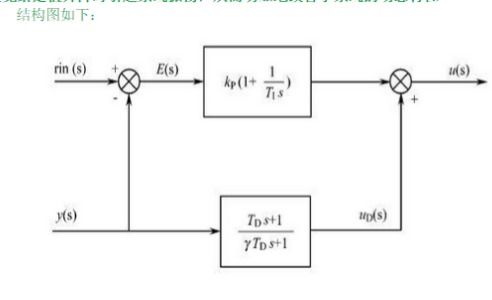
PID控制算法,即比例-积分-微分控制算法,是一种广泛应用于工业控制领域的经典控制算法。本文将详细介绍PID控制算法的原理、实现方法以及在各个领域的应用。
一、PID控制算法的原理
PID控制算法的核心思想是通过比例、积分和微分三个环节来调整控制器的输出,以达到对被控对象的精确控制。具体来说,PID控制算法的原理如下:
比例环节(Proportional):根据当前误差信号的大小,按比例调整控制器的输出。
积分环节(Integral):根据误差信号的累积值,调整控制器的输出,以消除稳态误差。
微分环节(Differential):根据误差信号的变化趋势,调整控制器的输出,以预测误差信号的未来变化,提高系统的动态性能。
二、PID控制算法的实现
PID控制算法可以通过多种编程语言实现,以下以C语言为例,介绍PID控制算法的实现方法。
1. C语言实现PID控制算法的基本步骤
初始化PID参数:包括比例系数Kp、积分系数Ki、微分系数Kd、积分上限和下限等。
计算误差:根据当前设定值和实际值计算误差。
计算比例、积分和微分项:根据误差和PID参数计算比例、积分和微分项。
计算控制器输出:将比例、积分和微分项相加,得到控制器输出。
更新参数:根据实际控制效果,调整PID参数,以提高控制精度。
2. C语言实现PID控制算法的代码示例
```c
include
// PID参数
double Kp = 1.0;
double Ki = 0.1;
double Kd = 0.01;
double integral = 0.0;
double last_error = 0.0;
// 计算PID控制器输出
double pid_control(double setpoint, double actual_value) {
double error = setpoint - actual_value;
double proportional = Kp error;
integral = Ki error;
double derivative = Kd (error - last_error);
last_error = error;
return proportional integral derivative;
int main() {
double setpoint = 100.0;
double actual_value = 90.0;
double output = pid_control(setpoint, actual_value);
printf(\





