霍夫曼树,数据压缩的利器

霍夫曼树（Huffman Tree）是一种用于数据压缩的树形结构，也被称为最优二叉树。它是由大卫·霍夫曼（David A. Huffman）在1952年发明的，用于寻找最短的平均长度的前缀编码。

霍夫曼树的基本思想是：将出现频率较高的字符分配较短的编码，而将出现频率较低的字符分配较长的编码。这样可以使得整个编码的平均长度最短，从而实现数据压缩。

霍夫曼树的构建过程如下：

1. 将所有的字符按照其出现的频率从高到低排序，并将它们视为叶子节点。

2. 从叶子节点开始，每次选取两个频率最低的节点，将它们合并为一个新节点，新节点的频率为这两个节点频率之和。将新节点插入到排序后的节点列表中，并重新排序。

3. 重复步骤2，直到所有节点合并为一个根节点。

4. 在合并的过程中，为每个新节点分配一个二进制编码，例如，左子节点为0，右子节点为1。

5. 最后，每个叶子节点就对应了一个唯一的二进制编码，这个编码就是该字符的霍夫曼编码。

霍夫曼树在数据压缩中有着广泛的应用，例如在JPEG、MP3等文件格式中都有使用。它能够有效地减少数据的大小，同时保证数据的完整性。

深入解析霍夫曼树：数据压缩的利器

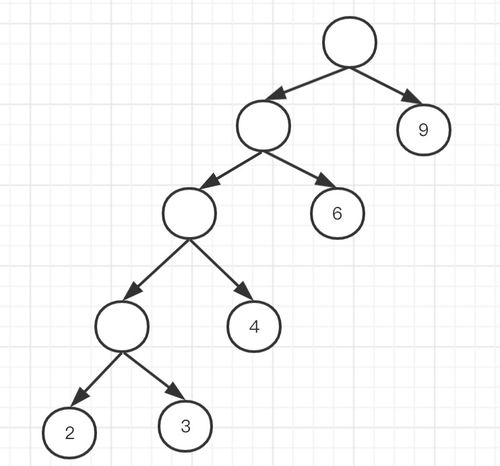
在数据压缩领域，霍夫曼树（Huffman Tree）是一种非常有效的数据结构。本文将深入解析霍夫曼树的基本原理、构建方法、应用场景以及与其它数据结构的异同。

一、什么是霍夫曼树？

霍夫曼树，也称为最优二叉树，是一种带权路径长度最短的二叉树。它通过贪心算法构建，主要用于最小化编码长度，从而实现数据的压缩。霍夫曼树在数据压缩领域扮演着重要角色，广泛应用于ZIP文件、JPEG图像压缩等领域。

二、霍夫曼树的构建方法

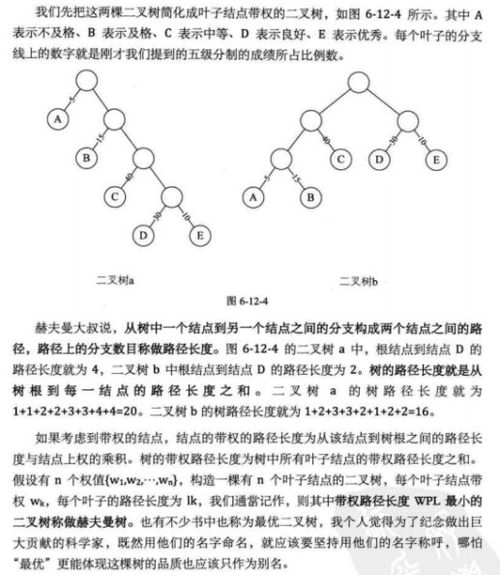
构建霍夫曼树的基本步骤如下：

统计频率：首先统计需要编码的每个符号的出现频率。

构建优先队列：根据符号频率构建优先队列，每个节点表示一个符号。

合并节点：从队列中取出两个频率最小的节点，合并为一个新节点，其频率为两个节点频率之和。重复这一过程，直到所有节点被合并为一棵完整的二叉树。

生成编码：从根节点开始，为每个分支赋值0或1，最终生成每个符号的二进制编码。

三、霍夫曼树的特点

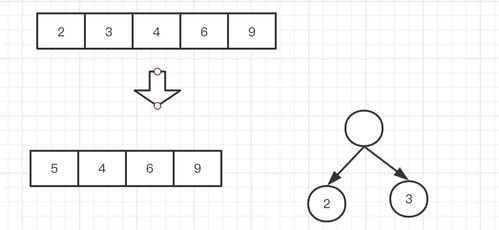
霍夫曼树具有以下特点：

结构不规则：霍夫曼树没有固定的树高，其结构取决于符号的频率分布。

带权路径长度最短：霍夫曼树通过贪心算法构建，使得带权路径长度最短，从而实现数据压缩。

前缀编码：霍夫曼树生成的编码具有前缀性质，即无一个编码是另一个编码的前缀。

四、霍夫曼树的应用

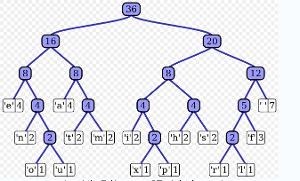
霍夫曼树在数据压缩领域有着广泛的应用，以下列举几个典型应用场景：

ZIP文件压缩：ZIP文件使用霍夫曼编码对文件进行压缩，提高存储效率。

JPEG图像压缩：JPEG图像压缩算法采用霍夫曼编码对图像进行压缩，减少图像文件大小。

文本压缩：霍夫曼编码可以应用于文本数据的压缩，提高存储和传输效率。

五、霍夫曼树与其它数据结构的异同

霍夫曼树、B树和决策树都是树形结构，但它们在结构、应用领域、构建方式和树的高度等方面存在显著差异：

结构上，霍夫曼树是不规则的二叉树，B树是多叉平衡搜索树，决策树是用于分类和回归的树结构。

应用领域，霍夫曼树用于数据压缩，B树用于数据库和文件系统索引，决策树用于机器学习的分类和回归任务。

构建方式，霍夫曼树通过贪心算法构建，B树通过节点数量的平衡来保持结构，决策树通过递归分裂数据集构建。

树的高度，霍夫曼树高度依赖于符号频率分布，B树高度较低且固定平衡，决策树高度不定。

节点内容，霍夫曼树节点存储符号及其频率，B树节点存储键值对或索引，决策树节点代表决策或条件。

霍夫曼树作为一种高效的数据压缩工具，在数据压缩领域具有广泛的应用。通过本文的介绍，相信大家对霍夫曼树有了更深入的了解。在实际应用中，我们可以根据具体需求选择合适的数据结构，以实现数据的高效存储和传输。