安培环路定理,稳恒磁场中的基本规律

安培环路定理（Ampère's circuital law）是电磁学中的一个重要定律，描述了电流与磁场之间的关系。它指出，穿过一个闭合回路的磁场线（即磁通量）与该回路所包围的电流成正比。数学表达式为：

∮B·dl = μ?I

其中： B 是磁场强度（单位：特斯拉，T）。 dl 是回路上的微小线段（单位：米，m）。 μ? 是真空的磁导率，约为 4π × 10?? T·m/A。 I 是穿过回路的电流（单位：安培，A）。

安培环路定理是电磁学中的基本定律之一，与法拉第电磁感应定律和麦克斯韦安培定律一起构成了麦克斯韦方程组，是描述电磁场与电荷和电流之间相互作用的基本方程。

安培环路定理：稳恒磁场中的基本规律

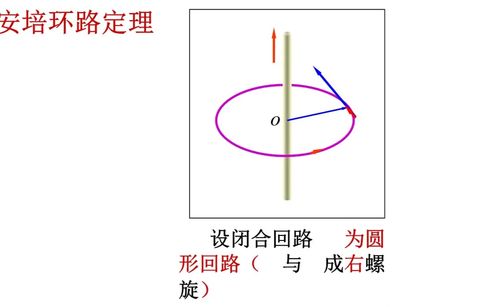
安培环路定理是电磁学中的一个重要定理，它描述了稳恒磁场中磁感应强度与电流之间的关系。本文将详细介绍安培环路定理的表述、证明及其应用。

安培环路定理的表述

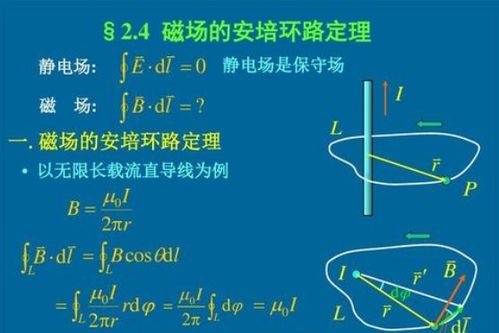
在稳恒磁场中，磁感应强度B沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流的代数和乘以磁导率μ。数学表达式为：

∮B·dl = μ(I)

其中，∮表示对闭合路径的线积分，B表示磁感应强度，dl表示闭合路径上的微小线段，μ表示磁导率，I表示闭合路径所包围的电流。

安培环路定理的证明

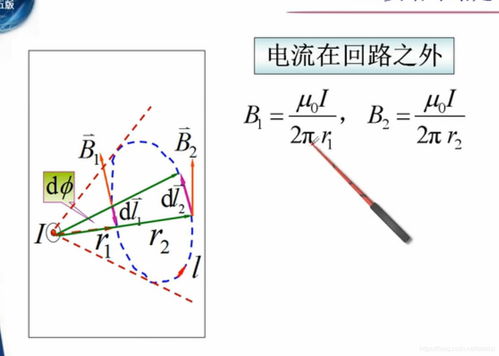
安培环路定理可以通过毕奥萨伐尔定律导出。毕奥萨伐尔定律描述了电流元对空间某点产生的磁场。根据毕奥萨伐尔定律，电流元I在空间某点P产生的磁感应强度dB为：

dB = (μ/4π) (I dL × r) / r^3

其中，dL表示电流元的长度，r表示电流元到点P的距离，×表示向量积。

将dB沿闭合路径L进行积分，得到磁感应强度B沿闭合路径L的线积分：

∮B·dl = ∮[(μ/4π) (I dL × r) / r^3]

由于dL × r = dr × r，且r^2 = r·r，上式可化简为：

∮B·dl = (μ/4π) ∮(I dr × r) / r^3

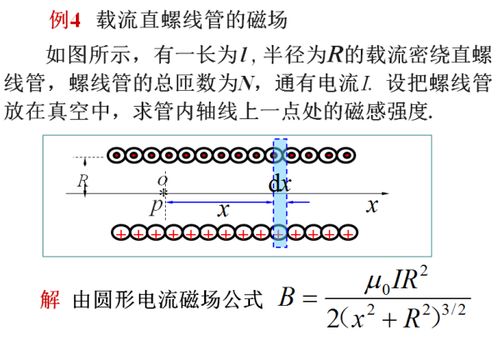
根据向量积的性质，上式可进一步化简为：

∮B·dl = (μ/4π) ∮(I dr) / r^2

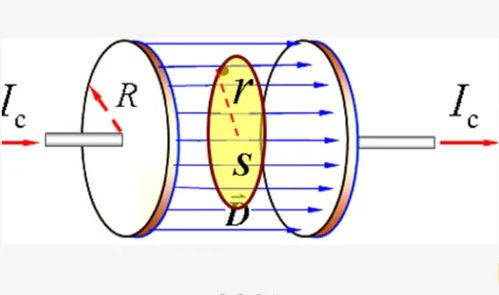
根据高斯散度定理，上式可转化为对闭合路径L所包围的体积V的积分：

∮B·dl = (μ/4π) ∫∫∫(I dv) / r^2

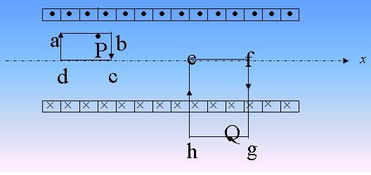
根据电流的连续性原理，上式可进一步化简为：

∮B·dl = (μ/4π) ∫∫∫(I) dv

上式即为安培环路定理的证明。

安培环路定理的应用

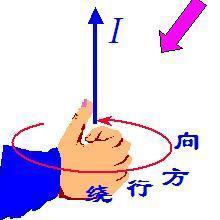
安培环路定理在电磁学中有着广泛的应用。以下列举几个应用实例：

1. 计算载流导线周围的磁场：通过安培环路定理，可以方便地计算载流导线周围的磁场分布。

2. 分析电流分布对磁场的影响：利用安培环路定理，可以分析电流分布对磁场的影响，从而优化电流分布。

3. 设计电磁装置：在设计和优化电磁装置时，安培环路定理可以帮助我们了解电流分布对磁场的影响，从而提高电磁装置的性能。

安培环路定理的物理意义

安培环路定理反映了稳恒磁场中磁感应强度与电流之间的关系。与静电场的环路定理相比，安培环路定理表明稳恒磁场是非保守场，不能引入势能。这意味着在稳恒磁场中，磁感应强度B沿闭合路径的线积分与路径无关，只与闭合路径所包围的电流有关。

安培环路定理是电磁学中的一个重要定理，它描述了稳恒磁场中磁感应强度与电流之间的关系。通过本文的介绍，我们了解了安培环路定理的表述、证明及其应用。安培环路定理在电磁学研究和工程应用中具有重要意义。