稀疏矩阵,什么是稀疏矩阵？

稀疏矩阵（Sparse Matrix）是一种特殊的矩阵，其中大部分元素都是零。在计算机科学中，稀疏矩阵通常用于表示网络图、线性方程组等数据结构，以节省存储空间和提高计算效率。稀疏矩阵的存储和操作方法与普通矩阵有所不同，需要特殊的算法和数据结构来处理。

稀疏矩阵的常见存储方法包括：

1. 三元组表示法（Compressed Sparse Row, CSR）：将非零元素及其行索引和列索引存储在一个列表中。例如，矩阵中的非零元素为 ，对应的行索引为 ，列索引为 ，则该矩阵可以表示为：

行索引: 列索引: 非零元素:

2. 三元组列表示法（Compressed Sparse Column, CSC）：与CSR类似，但非零元素及其行索引和列索引按列排序。例如，上述矩阵的CSC表示为：

行索引: 列索引: 非零元素:

3. 三元组对角线表示法（Diagonal Storage）：将非零元素及其行索引和列索引按对角线顺序存储。例如，上述矩阵的对角线表示为：

行索引: 列索引: 非零元素:

稀疏矩阵的操作方法包括：

1. 矩阵加法：将两个稀疏矩阵的非零元素相加，同时更新行索引和列索引。

2. 矩阵乘法：将一个稀疏矩阵与一个普通矩阵相乘，或者两个稀疏矩阵相乘。需要特殊的算法来处理非零元素的乘积。

3. 矩阵转置：将稀疏矩阵的行索引和列索引互换，同时更新非零元素的存储顺序。

稀疏矩阵的存储和操作方法可以提高计算机处理大规模数据时的效率和准确性。在实际应用中，稀疏矩阵通常用于科学计算、图像处理、机器学习等领域。

稀疏矩阵：高效存储与运算的秘密武器

什么是稀疏矩阵？

稀疏矩阵是一种特殊的矩阵，其大部分元素为0。在现实世界中，许多矩阵都是稀疏的，例如网络图、图像处理、科学计算等领域。由于稀疏矩阵中非零元素较少，因此如何高效地存储和运算稀疏矩阵成为了一个重要的研究方向。

稀疏矩阵的存储方法

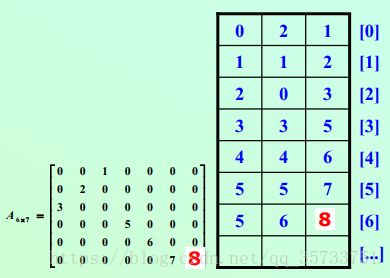
三元组表（COO格式）：使用三个数组分别存储非零元素的行索引、列索引和值，这种存储方式简单直观，但插入和删除操作较为复杂。

压缩稀疏行（CSR格式）：将矩阵压缩成三个一维数组，分别存储非零元素的行索引、列索引和值，这种存储方式适合进行矩阵乘法运算。

压缩稀疏列（CSC格式）：与CSR格式类似，但顺序相反，适合进行矩阵转置运算。

十字链表：使用链表结构存储稀疏矩阵，每个节点包含行索引、列索引、值以及指向同一行和同一列的下一个节点的指针，这种存储方式适合进行矩阵加法运算。

稀疏矩阵的运算

稀疏矩阵加法：通过遍历两个稀疏矩阵的非零元素，将对应位置的元素相加，若相加结果不为0，则保留该元素；若为0，则删除该元素。

稀疏矩阵减法：与加法类似，但将对应位置的元素相减。

稀疏矩阵乘法：通过遍历两个稀疏矩阵的非零元素，计算对应位置的乘积，若乘积不为0，则保留该元素；若为0，则删除该元素。

稀疏矩阵转置：将稀疏矩阵的行索引和列索引交换，并重新组织数据。

稀疏矩阵的应用

图像处理：在图像处理中，稀疏矩阵可以用于表示图像的像素值，从而提高图像处理算法的效率。

网络分析：在社交网络、交通网络等领域，稀疏矩阵可以用于表示网络结构，从而进行网络分析。

科学计算：在物理、化学、生物等领域，稀疏矩阵可以用于表示复杂的计算模型，从而提高计算效率。

数据挖掘：在数据挖掘中，稀疏矩阵可以用于表示数据集，从而进行高效的数据分析。

稀疏矩阵是一种高效存储和运算数据的方法，在许多领域都有广泛的应用。随着计算机技术的不断发展，稀疏矩阵的研究和应用将越来越广泛，为各个领域带来更多的便利。