信息增益,机器学习中的核心概念

信息增益（Information Gain）是决策树算法中用于选择分割节点的标准之一。它衡量了在给定数据集的条件下，某个特征对于分类目标的预测能力。

信息增益的计算公式如下：

$$ text{信息增益} = text{父节点的熵} text{子节点的熵加权平均} $$

其中，熵（Entropy）是一个衡量数据集混乱程度的指标，计算公式为：

$$ text{熵} = sum_{i=1}^{n} p_i log_2 p_i $$

其中，$ p_i $ 是第 $ i $ 类样本出现的概率。

信息增益的直观意义是：选择一个特征作为分割节点，可以使得数据集的混乱程度降低多少。信息增益越大，说明该特征对于分类目标的预测能力越强，因此应该优先选择该特征作为分割节点。

需要注意的是，信息增益存在一个问题，即它倾向于选择具有更多类别的特征。为了解决这个问题，可以使用信息增益率（Gain Ratio）作为选择分割节点的标准。

信息增益：机器学习中的核心概念

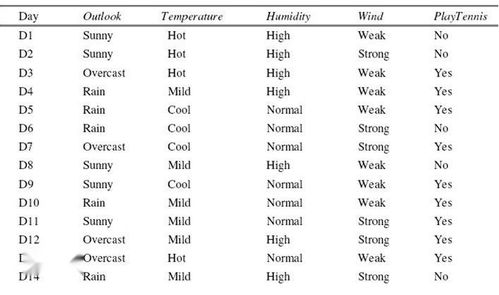
在机器学习领域，信息增益是一个至关重要的概念，尤其在决策树算法中扮演着核心角色。信息增益用于评估一个特征对数据集的划分能力，即该特征在区分不同类别或预测目标变量时的有用程度。

什么是信息增益？

信息增益（Information Gain）是信息论中的一个概念，它描述了在给定一个特征的情况下，数据集的不确定性减少的程度。具体来说，信息增益可以理解为在已知某个特征的情况下，数据集的熵（Entropy）减少的量。

信息增益的计算方法

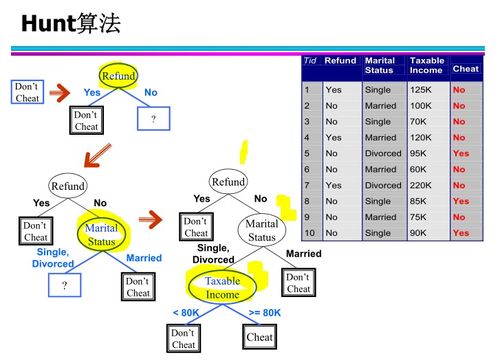
信息增益的计算公式如下：

\\[ IG(S, A) = Entropy(S) - \\sum_{v \\in Values(A)} \\frac{|S_v|}{|S|} Entropy(S_v) \\]

其中：

- \\( S \\) 是原始数据集。

- \\( A \\) 是待评估的特征。

- \\( Values(A) \\) 是特征 \\( A \\) 的所有可能取值。

- \\( S_v \\) 是在特征 \\( A \\) 取值为 \\( v \\) 的情况下，数据集 \\( S \\) 的子集。

- \\( |S| \\) 是数据集 \\( S \\) 的样本数量。

- \\( |S_v| \\) 是子集 \\( S_v \\) 的样本数量。

通过计算信息增益，我们可以得到每个特征对数据集的划分能力，从而选择最优的特征进行分类或回归分析。

信息增益在决策树中的应用

在决策树算法中，信息增益被用来选择最优的特征进行节点划分。具体步骤如下：

1. 计算数据集的熵。

2. 对于每个特征，计算其信息增益。

3. 选择信息增益最大的特征作为当前节点的划分依据。

4. 根据该特征将数据集划分为若干个子集。

5. 递归地对每个子集进行相同的操作，直到满足停止条件。

通过这种方式，决策树可以有效地对数据进行分类或回归分析，并且具有较好的泛化能力。

信息增益的局限性

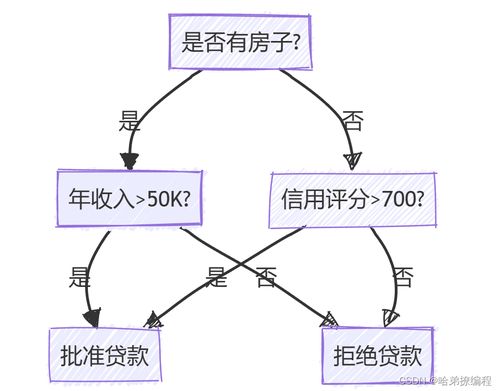
尽管信息增益在决策树算法中具有重要作用，但它也存在一些局限性：

1. 信息增益容易受到特征取值数量和分布的影响。当特征取值数量较多或分布不均匀时，信息增益的计算结果可能不够准确。

2. 信息增益无法直接反映特征之间的关联性。在某些情况下，即使两个特征的信息增益较高，它们之间也可能没有明显的关联。

3. 信息增益在处理连续特征时，需要将其离散化，这可能导致信息损失。

信息增益是机器学习中一个重要的概念，尤其在决策树算法中具有核心地位。通过计算信息增益，我们可以选择最优的特征进行数据划分，从而提高模型的分类或回归性能。然而，信息增益也存在一些局限性，需要在实际应用中加以注意。