优先队列,什么是优先队列？

优先队列（Priority Queue）是一种抽象数据类型，它类似于队列，但每个元素都关联着一个优先级。在优先队列中，元素被按照优先级顺序进行排列，而不是按照它们被插入的顺序。这意味着，当从优先队列中取出元素时，具有最高优先级的元素总是先被取出。

优先队列的主要操作包括：

1. 插入（Insert）：向优先队列中添加一个元素。插入操作可能需要根据元素的优先级将其放置在队列的适当位置。

2. 删除（Delete）：从优先队列中移除具有最高优先级的元素。在最大优先队列中，这通常是移除具有最大值的元素；在最小优先队列中，这通常是移除具有最小值的元素。

3. 查找（FindMax/FindMin）：返回具有最高优先级的元素，但不从队列中移除它。

4. 更新（Update）：改变队列中某个元素的优先级。

优先队列通常使用二叉堆（Binary Heap）来实现，二叉堆是一种特殊的二叉树，它满足堆性质（Heap Property）：对于任何节点，其值都大于或等于其子节点的值（最大堆）或小于或等于其子节点的值（最小堆）。

在实际应用中，优先队列被广泛用于许多算法中，例如：

Dijkstra算法：用于寻找图中两个顶点之间的最短路径。 Prim算法：用于找出无向加权图的最小生成树。 Huffman编码：用于数据压缩。

这些算法都需要一个高效的数据结构来维护元素的优先级，而优先队列正好提供了这样的功能。

什么是优先队列？

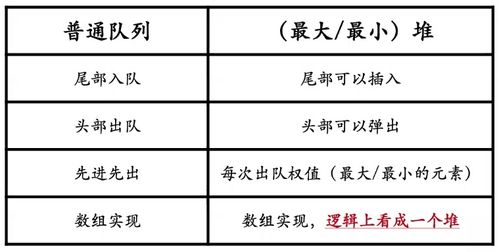
优先队列是一种先进先出（FIFO）的数据结构，但它与传统队列不同的是，元素在队列中的位置是根据其优先级来决定的。在优先队列中，总是具有最高优先级的元素最先被处理。这种数据结构在许多算法和系统中都有广泛的应用，如任务调度、资源分配、网络流量管理等。

优先队列的基本概念

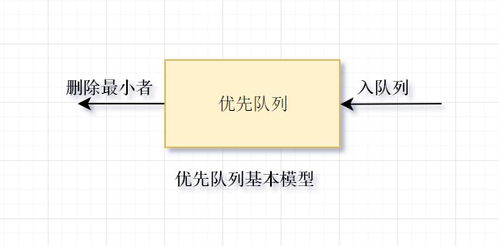
优先队列通常使用堆（Heap）这种数据结构来实现。堆是一种特殊的树形数据结构，它满足以下性质：

最大堆（Max-Heap）：每个父节点的值都大于或等于其所有子节点的值。

最小堆（Min-Heap）：每个父节点的值都小于或等于其所有子节点的值。

在优先队列中，通常使用最小堆来实现，因为这样可以保证每次从队列中取出的是具有最高优先级的元素。

优先队列的常用操作

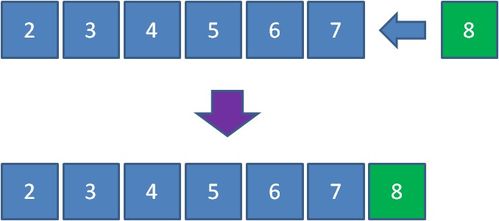
优先队列提供了以下基本操作：

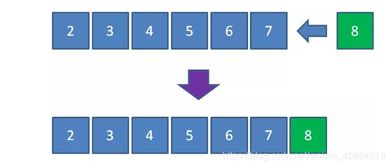
插入（Insert）：将一个新元素插入到优先队列中。

删除（Delete）：从优先队列中删除具有最高优先级的元素。

获取最大/最小元素（GetMax/GetMin）：获取优先队列中具有最高优先级的元素，但不删除它。

判断队列是否为空（IsEmpty）：判断优先队列是否为空。

获取队列大小（Size）：获取优先队列中元素的数量。

优先队列的实现

优先队列可以使用多种方式实现，以下列举几种常见的实现方法：

数组实现：使用数组来存储堆，通过调整数组元素的位置来维护堆的性质。

链表实现：使用链表来存储堆，通过指针来维护堆的结构。

平衡二叉树实现：使用平衡二叉树（如AVL树、红黑树）来实现堆，以保证堆的平衡性。

在C 中，可以使用STL中的`priority_queue`容器来实现优先队列，它底层使用最大堆来实现。

优先队列的应用

优先队列在许多领域都有广泛的应用，以下列举一些常见的应用场景：

任务调度：在多线程或多进程环境中，可以使用优先队列来调度任务，确保高优先级的任务先被执行。

资源分配：在资源受限的环境中，可以使用优先队列来分配资源，确保高优先级的资源先被分配。

网络流量管理：在计算机网络中，可以使用优先队列来管理网络流量，确保高优先级的流量先被处理。

图算法：在图算法中，如Dijkstra算法和A算法，可以使用优先队列来存储待处理的节点，并按照节点到目标节点的预估成本进行排序。

优先队列是一种高效的数据结构，在许多领域都有广泛的应用。通过使用堆来实现，优先队列可以保证每次从队列中取出的是具有最高优先级的元素。在实际应用中，可以根据具体需求选择合适的实现方式和应用场景。

- 优先队列

- 堆

- 数据结构

- 算法

- 应用场景